II. Calculs
Effets gyroscopiques
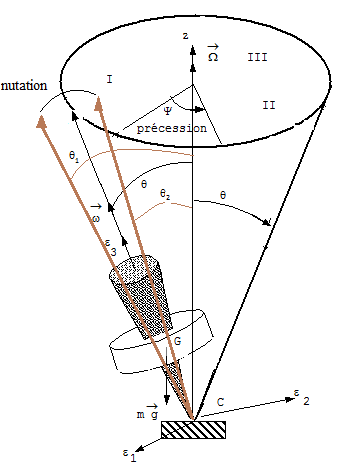
Les deux principaux phénomènes observables sur un gyroscope sont la nutation et la précession.
La force de nutation est une force perpendiculaire à l’axe du rotor qui résiste au mouvement. On mesure l’angle de nutation par rapport à l’axe verticale z.
La vitesse de précession correspond quant à elle au nombre de tours que fait le gyroscope sur lui-même en 1 seconde suivant un angle constant. Le gyroscope décrit au cours du temps un cône.
Caractéristiques techniques de notre gyroscope
| Gyroscope Dimensions | |||||
| Total Weight: | 345g | ||||
| Gyroscope weight without motor : | 145g | ||||
| Weight of brass disk alone (with shaft) : | 112g | ||||
| Aluminium casing, bearings and shaft weigh : | 33g | ||||
| Outer frame diameter: | 62.5mm | ||||
| Brass disk diameter: | 53mm | ||||
| Brass disk thickness: | 12mm | ||||
| Motor length: | 58.2mm | ||||
| Motor diameter (at largest point): | 28.1mm | ||||
| RPM | 12000 | ||||
| Electrical characteristics | |||||
| Motor Amps (at start up): | 2.5 amps | ||||
| Motor Amps (at full rpm): | 0.5 amps | ||||
| Motor/gyroscope speed: | 12,000 rpm~ | ||||
| Motor Voltage with standard batteries: | 5.8 volts | ||||
| Nominal Motor Voltage: | 6 volts | ||||
| Physics | |||||
| Moment of Interia: | 0.000055 kg.m2 | ||||
Tout est disponilbe sur le site gyroscope.com
Formulaire (pour la suite)
𝜏⃗ : Moment du gyroscope
𝐼⃗ : Moment d’Inertie
𝐿⃗ : Moment cinétique
Ω𝑠=−𝑚𝑔𝑙𝐼𝜔
Ω𝑠 : Vitesse angulaire (effet gyroscopique) de la précession
l : Distance sol/centre
F : Nutation -> tendance du gyroscope à maintenir son axe (vertical)
𝐹=−2𝑚𝜔𝑠𝑉𝑟
𝑉𝑟= 𝜔𝑟sin(𝜃)𝑅
m : Masse par unité d’arc -> m = 𝑀2𝜋
𝜃 : Angle entre l’axe et la circonférence du rotor
𝜔𝑠 : Vitesse angulaire de la précession
𝑉𝑟 : Composante de vitesse vers l’axe central
Moment d'inertie
Le premier calcul réalisé était celui du moment d’inertie du gyroscope. L’inertie représente la tendance d’un objet à garder sa vitesse et à résister aux changements. Ce moment est donc à la base des effets gyroscopiques puisqu’un gyroscope résiste naturellement à un changement d’orientation.
A l’aide d’une double intégration, j’ai réussi à trouver le moment d’inertie de notre gyroscope avec cette formule :
![]()
Où D est la surface du rotor. Suite du calcul :
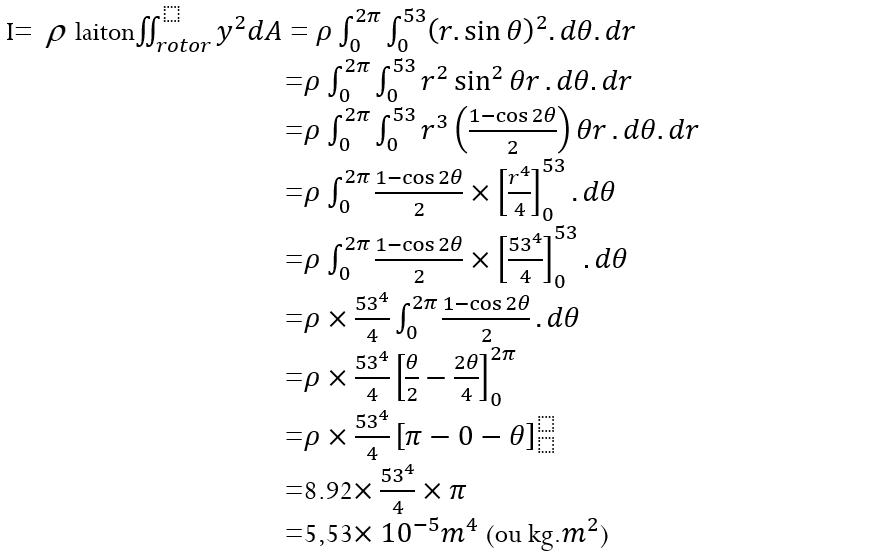
Le résultat est d’ailleurs correct puisqu’après avoir contacté le support de gyroscope.com pour réparer notre gyroscope, un ingénieur nous a donné sa valeur du moment d’inertie qui est I=5.93*10^-5 m^4
Vitesse angulaire de précession
Cette vitesse correspond au nombre de tour que le gyroscope fait sur lui-même en une seconde. On observe qu’elle ne dépend pas de son angle d’inclinaison :
\({ Vr=\ \frac{mgl}{I.\omega}}\)
\({ Vr=\ \frac{145\ast{10}^{-3}\ast9.81\ast12{\ast10}^{-2}}{5.53{\ast10}^{-5}\ast1256.64}=2.45\ rad.s^{-1}}\)
\({ Vr=0.39\ tr.s^{-1}}\)
En d’autres termes, il lui faut environ 2.5 secondes pour faire un tour sur lui-même.
Force de nutation
Le calcul de la force de nutation permet de connaitre la force de résistance maximale du gyroscope suivant son angle d’inclinaison. D’après une formule, on obtient ce résultat :
\({ r=\ \omega_r\sin{\left(\theta\right)}R}\)
\({ r=\ 1256,64\times\sin(20)\times26,5\times10-3}\)
\({ r=\ 11,39\ m.s^{-1}}\)
\({ F=2\times\frac{m}{2\pi}\times\ \omega_s\times\ V}\)
\({ F=2\times\frac{112\times{10}^{-3}}{2\pi}\times2,45\times11,39}\)
\({ F=0.99\ N}\)
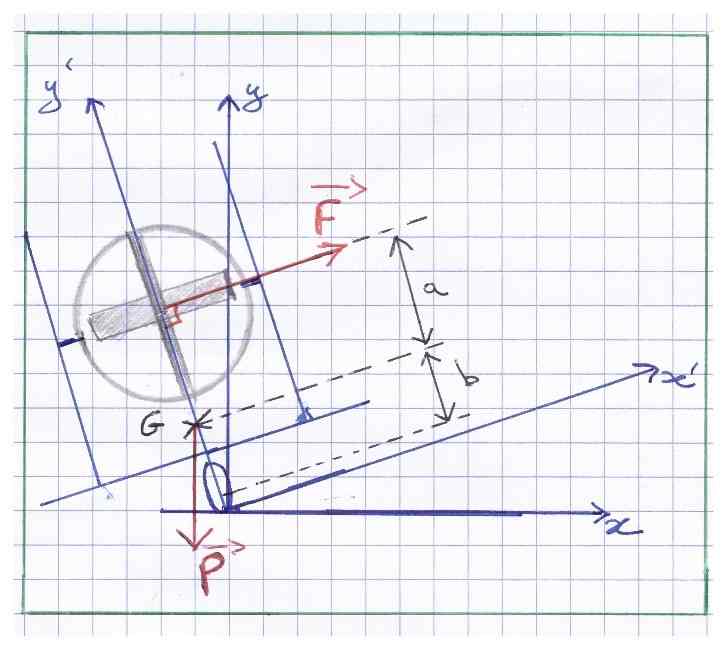
Le reste du travail consiste donc à vérifier que cette force théorique est suffisante pour maintenir le train à l’équilibre. J’ai donc fait un schéma simplifié du train et j’ai appliqué le PFS. On en déduit l’équation de la force théorique nécessaire au maintien en équilibre du train au centre de gravité du gyroscope suivant l’inclinaison.
Le calcul du centre de gravité n’est pas nécessaire car après simplification de l’équation de F on obtient a+b qui correspond à la distance entre les 2 grands centres de gravités connus : la structure du train et le gyroscope.
Le calcul du centre de gravité n’est pas nécessaire car après simplification de l’équation de F on obtient a+b qui correspond à la distance entre les 2 grands centres de gravités connus : la structure du train et le gyroscope :
\({ F=\frac{b.sin\alpha.mg}{a+b}}\)
(voir annexe 1 pour les détails du calcul)
Annexe 1, Calculs détaillés :
Ensuite à l’aide d’un tableau Excel j’ai comparé les valeurs théoriques nécessaires et fournies par le gyroscope suivant l’inclinaison (pas de 0.1°). Ce qui nous donne ces deux courbes significatives ->
Vous pouvez télécharger le fichier excel ici :
On constate que les calculs confirment la pratique ; le gyroscope ne fournit pas assez de force pour maintenir en équilibre le train.
En inversant l’équation, on peut trouver la vitesse de rotation nécessaire au maintien du train :
\({ N_r=\frac{2\pi*F}{2*m*\omega_s*\sin{\left(\theta\right)}*R}\ast2}\)
\({ N_r=\ 19152\ tr.s^{-1}}\)
Il était difficile de prouver ce résultat sans faire surchauffer le moteur, mais nous avons pris le risque. On s’est arrêté à 18800 tr/s et le train était stable pour un temps beaucoup plus long. Le résultat de ce calcul est donc fortement probable et proche de la réalité. Seulement cette vitesse de rotation est trop élevée pour notre moteur. Notez que nous avons utilisé un tachymètre pour mesurer la vitesse de rotation du gyroscope. Pour ce faire, il fallait fixer une petite surface réfléchissante au laser de l’appareil sur le rotor.
Résultats du test :
|
Volts |
Ampères |
RPM |
Temps en équilibre (s) |
|
6 |
0,7 |
13000 |
14,53 |
|
8 |
0,8 |
18800 |
28,1 |